VSE ProjectionViewer Dokumentation – Documentation for LenIT

ProjectionViewer Beschreibung

Der ProjectionViewer ermöglicht die visuelle Inspektion ihrer Daten mittels multivariater Projektionen. Damit wird der Datensatz nicht nur vollständig dargestellt, sondern es werden auch Zusammenhänge erkennbar, an welchen mehrere Dimensionen bzw. Spalten ihrer Daten beteiligt sind.
Oder im Klartext, sie können leicht globale Zusammenhänge finden.

Unter anderem, bietet ihnen dieses Modul folgende Analysefunktionen an:
– manuelle Inspektionen
– Optimierten Mengen an guten Projektionen
– Star Coordinates, Radial Visualization und Othographic Star Coordinates
– Generelle Projektive Karten
– Visuelles Clustering

Unsere manuelle Inspektion erlaubt es Ihnen interaktiv nach interessanten Projektionen zu suchen.
Wozu? Weil es unendlich viele solcher Projektionen gibt: Unsere manuelle Inspektion hilft Ihnen schnell und sicher interessante Projektionen zu finden.

Wir haben noch weitere Werkzeuge diesbezüglich für Sie:
Sie können im ProjectionViewer eine Menge an Projektionen vorberechnen lassen, welche interessante Strukturen Ihrer Daten zeigen. Nutzen sie dazu unsere Funktion der „Optimierten Mengen an guten Projektionen“. Natürlich bieten wir Ihnen auch “PCA“ und “MDS-eske“ Konfigurationen an, und vieles mehr…

Auch bieten wir Ihnen verschiedene Projektionsarten an, wie den:
– Star Coordinates
– Radial Visualization
– Othographic Star Coordinates

Ganz allgemein haben Sie auch Zugriff auf unsere „Generelle Projektive Karten“, was es den Fachexperten unter Ihnen ermöglicht den Raum der linearen und nicht-linearen multivariaten Projektion vollständig zu explorieren.

Zusätzlich bieten wir Ihnen interessante visuelle Linsen an, wie unsere „Polyfokale Magische Linse“ und unsere „Projektive Magische Linse“, um weitere Eigenschaften Ihrer Daten interaktiv Aufzudecken.

Darüber hinaus haben wir spannende Werkzeuge für das Visuelle Clustering Ihrer Daten und vieles mehr. Insgesamt ist unser ProjectionViewer ein sehr starkes und mächtiges Werkzeug der Datenanalyse.

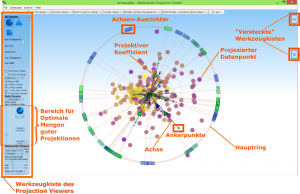
ProjectionViewer Übersicht

ProjectionViewer Releases

ProjectionViewer Funktionen

Star Coordinates

Wenn sie hier drücken, erhalten sie sogenannte Star Coordinates. Das bedeutet das die dreieckigen projektiven Koeffizienten im Mittelpunkt angeordnet sind. Für die Fachexperten unter Ihnen: Es bedeutet das die projektiven Koeffizienten auf 0 gesetzt werden und wir damit eine lineare multivariante Projektion verwenden.

Orthographic Star Coordinates

Wenn sie hier „Orthographie-erhaltend“ auswählen und ihre Manuelle Exploration ausführen, dann werden sie feststellen das die Anderen Achsen sich eigenständig mit ausrichten. Im Klartext, die Achsen scheinen nicht nur miteinander gekoppelt zu sein, sie sind es auch. Wir nennen solche Projektionen „Orthographic Star Coordinates“. Ihr Zweck ist es, zu verhindern, das sich Abstandsinformationen ihrer Daten innerhalb der Projektion zu stark verändern.

Wie ist das zu verstehen?
Stellen sie sich einen Sonnenuntergang und einen kleinen Gartenzwerg vor: Der Schatten des Gartenzwerges erscheint riesig zu sein, obwohl der Gartenzwerg selbst eher klein ist. In diesem Bild, entspricht die Länge ihres Gartenzwerges dem Abstand ihrer Daten, während sein Schatten genau dem Abstand in der Projektion entspricht. Schauen sie nun auf den Schatten ihres Gartenzwerges,
würden sie denken, das sie es mit einem sehr großen Gartenzwerg zu tun haben. Dem ist natürlich weiterhin nicht so!

Solche Verzerrungen treten in Projektionen leider sehr oft auf. Der Trick um solche Verzerrungen zu minimieren, ist es, die Position der Sonne nun so zu wählen, das der Schatten ihres Gartenzwerges genauso Groß erscheint wie ihr Gartenzwerg selbst.

In unserem Bild mit dem Gartenzwerg, entspricht die Position der Sonne der Konfiguration der Achsen unserer Achsenanordnung.
Die „Orthographic Star Coordinates“ wählen die Achsen nun automatisch so, das der Schatten ihrer Daten in der Projektion ähnlich groß ist, wie die Länge ihrer originalen Daten zueinander. Nun haben wir solche ungünstigen Verzerrungen in der Projektion erfolgreich reduziert.

Radial Visualizations

Wenn sie hier drücken, erhalten sie sogenannte Radial Visualizations. Das bedeutet das die dreieckigen projektiven Koeffizienten auf dem Hauptring angeordnet sind. Für die Fachexperten unter Ihnen: Es bedeutet das die projektiven Koeffizienten auf 1 gesetzt werden und wir damit eine nicht-lineare multivariate Projektion verwenden.

Radial Layout

Wenn sie hier drücken, dann werden die Achsen radial, also Winkeltreu, angeordnet, etwas einfacher gesagt, wir platzieren ihre Ankerpunkte auf einen Kreis, zur besseren Übersicht für sie.

Manuelle Exploration

Der ProjectionViewer ermöglicht die visuelle Inspektion ihrer Daten mittels multivarianter Projektionen. Damit wird der Datensatz nicht nur vollständig dargestellt, sondern es werden auch Zusammenhänge erkennbar, an welchen mehrere Dimensionen bzw. Spalten ihrer Daten beteiligt sind. Oder im Klartext, sie können leicht globale Zusammenhänge finden.

Eine Eigenschaft solcher multivarianter Projektionen ist, es gibt unendlich viele davon:
Wie können wir nun interessante Projektionen finden?

Um den Projektionsraum nach interessanten Projektionen zu durchsuchen, bietet Ihnen das Modul die Möglichkeit einer so genanten manuellen Inspektion:
Was ist dies? Nun, zunächst einmal sehen sie eine Vielzahl an sternförmig zulaufenden Linien welche wir Achsen nennen. An deren Ende befinden sich Punkte, welche wir Ankerpunkte nennen. Sie müssen nun wissen, das die Ausrichtung der Achsen und Platzierung der Ankerpunkte die Eigenschaften bestimmen, wie ihre Daten projiziert werden. Je langer oder kürzer eine Achse, oder auch wen sie deren Winkel ändern würden, desto anders sähe ihre Projektion aus. Nun wird auch klar, das es unendlich viele solcher Projektionskonfigurationen geben kann.

Sie können aber selbstständig die Ankerpunkte beliebig im Raum interaktiv positionieren, und so die Eigenschaften ihrer Projektion bestimmen. Wir nennen dies eine manuelle Exploration. Sie ermöglicht es ihnen interessante Projektionen ihrer Daten zu finden. Dazu verschieben sie die Ankerpunkte nach belieben per Drag&Drop.

Um einfach nur den Winkel ihrer Ankerpunkte zu ändern, ohne aber die Länge der Achsen selbst, können sie die rechteckigen Boxen am Rande interaktiv verwenden; wir bezeichnen sie als Achsen-Ausrichter. Wir denken, die Achsenausrichter sind ein weiteres bequemes Werkzeug und hoffen das es ihnen die Manuelle Exploration zusätzlich vereinfacht.

Optimierte Menge an guten Projektionen

Sie können im ProjectionViewer eine Menge an Projektionen vorberechnen lassen, welche interessante Strukturen ihrer Daten zeigen. Wir nennen das Konzept die Optimierte Menge an guten Projektionen. Die Idee ist, das sie nicht manuell die einzelnen Achsen so wählen müssen bis sie eine interessante Struktur finden, sondern das der ProjectionViewer ihnen spannende Achsenkonfigurationen vorberechnen kann.

Zur Berechnung solcher interessanten Projektionen drücken sie diesen Button um den Berechnungsprozess zu starten. Übrigens, sie brauchen dies pro Datensatz nur einmal berechnen lassen. Wir speichern ihre Ergebnisse für zukünftige Session automatisch. Diese einmalige Berechnung selbst kann je nach Größe des Datensatzes ein paar Sekunden oder Minuten dauern. Die Parameter an dieser Stelle welche den Berechnungsprozess steuern, sind bereits optimal gewählt, und können so belassen werden.

Sobald die Berechnung abgeschlossen ist, sehen sie einen neuen Slider und eine weitere Auswahlmöglichkeit. Sie bietet ihnen nun die Möglichkeit die einzelnen vorberechneten Projektionen nacheinander zu betrachten. Sie können entweder jede Projektion einzeln betrachten, dazu wählen sie die Auswahl „Stufe“, oder sie können durch ihre Projektionen hindurch animieren, dazu wählen sie die Auswahl „linear Interpoliert“.

Wenn sie nun den Slider verwenden, sehen sie – je nach Auswahl – die einzelnen Projektionen oder eine Animation dieser optimierten Menge an guten Projektionen.

Hier noch ein kleiner Hinweis für die absoluten Fachexperten unter ihnen:
Selbstverständlich können sie auch ähnliche Projektionen über eine Hauptkomponentenanalyse (engl. Principal Component Analysis) berechnen. Dazu klicken sie einfach auf den „PCA verfügbar“ Button und markiere die Checkbox. Nun können sie mit den Slider über die PCA-basieten Projektionen explorieren.

Zwischen den optimalen Projektionen und den PCA-basierten, schalten sie um, durch die Checkbox. Der Vorteil unserer optimierten Projektionen gegenüber den PCA-basierten ist, dass die Optimierten mit einer Anzahl von “n-halbe“ viele Projektionen auskommen, während die PCA-basierten “n-quadrat“ viele benötigen und zudem Gaus-verteilte Daten voraussetzen. “n“ ist hier ihre Anzahl an Dimensionen bzw. Spalten ihres Datensatzes. Beide Mengen zeigen den Projektionsraum vollständig.

Generelle Projektive Karten

Multivariate Projektionen haben sehr erstaunliche aber oft wenig greifbare Eigenschaften. Schauen sie das Video unserer Orthographic Star Coordinates an, dann haben sie schon eine Ahnung davon, das sich Längen verändern können in der Projektion.

Eine weitere solcher Eigenschaft ist, das es lineare und nicht-lineare Projektionen gibt. Der Unterschied ist, das die Verzerrungen der Längen der Daten sich je nach Lage der Daten im Datenraum auch noch verändern können. Sicherlich, ein sehr abstraktes Konzept!

Wie dem auch sei, trifft dieser Effekt zu, sprechen wir von nicht-linearen Projektionen, sonst von linearen Projektionen.

Zwischen nicht-linearen Projektionen und linearen Projektion können sie selbständig blenden mit unserem Tool, falls sie es möchten: Wie das? Sie sehen kleine Dreiecke entlang ihrer Achsen. Wir nennen sie projektive Koeffizienten. Sind diese im Mittelpunkt, sind die Koeffizienten alle 0, und wir erhalten lineare Projektionen.

Sind diese auf dem Hauptring, sind die Koeffizienten alle 1, und wir erhalten nicht-lineare Projektionen. Sind sie irgendwo dazwischen, haben sie einen Wert zwischen 0 und 1, oder mehr. Je größer ihr Wert, desto nicht-linearer ist die Projektion. Sie können dies also frei steuern. Wir bezeichnen dieses Konzept als „Generelle Projektive Karten“.

Übrigens, sind diese Dreiecke im Mittelpunkt platziert, erhalten wir Star Coordinates.Sind sie auf dem Hauptkreis platziert, erhalten wir Radial Visualization. Also wäre dies ein guter Zeitpunkt für Sie, sich auch einmal unsere Videos zu den Star Coordinates und den Radial Visualization anzuschauen.

Projective (Min Distance Error)

Wenn Sie den Punkt „Projective (Min Distance Error)“ auswählen und eine manuelle Exploration durchführen, werden Sie feststellen, dass die dreieckigen projektiven Koeffizienten sich selbstständig anpassen.

Offensichtlich scheinen die projektiven Koeffizienten miteinander gekoppelt zu sein. Und tatsächlich sind sie es. Ihr Zweck besteht darin, zu verhindern, dass die Entfernungsinformation der Daten innerhalb der Projektion zu stark verzehrt wird.

Das Konzept ähnelt unserem Konzept der „Orthographic Star Coordinates“. Sehen sie sich also gerne auch unser Video zu den „Orthographic Star Coordinates“ an.

Im Konzept unserer „Projective (Min Distance Error)“ jedoch, bleibt die Achsenkonfiguration an sich unberührt. Stattdessen werden die projektiven Koeffizienten optimal ausgewählt, so dass Verzerrungen minimiert werden.

Projective Magic Lens

Wählen sie hier „Projective Magic Lens“, dann können sie in der Projektion mit halten der rechten Maustaste eine visuelle Linse einblenden lassen.

Dessen Größe können sie – bei gehaltener rechter Maustaste – mit dem Scrollrad vergrößern oder verkleinern. Die Stärke der Wirkung der Linse können sie über den Regler hier einstellen.

Der Nutzen dieser Linse ist es Verzerrungen ihrer dargestellten Daten zu minimieren, ohne jedoch ihre gewählte Achsenkonfiguration zu verändern. Dazu wählt die Linse die Dreieckig dargestellten projektiven Koeffizienten in geeigneter Weise aus. Falls sie noch nicht Wissen was projektive Koeffizienten sind, dann schauen sie sich doch gerne gleich unser Video zu den „Generelle Projektive Karten“ an.

Polyfocal Magic Lens

Wählen sie hier „Polyfocal Magic Lens“, dann können sie in der Projektion mit halten der rechten Maustaste eine visuelle Linse einblenden lassen.

Dessen Größe können sie – bei gehaltener rechter Maustaste – mit dem Scrollrad vergrößern oder verkleinern. Die Stärke der Wirkung der Linse können sie über den Regler hier einstellen.

Der Nutzen dieser Linse ist es, Ihre Projektion bei Bedarf optisch zu vergrößern.